树上 k 祖先问题

$k$ 祖先问题

$k$ 祖先问题（Level Ancestor Problem）是静态树的重要问题之一。给定一棵树和若干个询问 $(u, k)$，要求结点 $u$ 的第 $k$ 个祖先结点。

离线情景下的 $k$ 祖先问题存在一个简单的 $O(n+q)$ 的算法：在 dfs 的过程中维护一个记录祖先的栈，然后在每个结点处回答和这个结点有关的所有询问；在线情景下有基于倍增的 $O(n\log n)-O(\log n)$ 算法，基于长链剖分的 $O(n)-O(\log n)$ 算法和 $O(n\log n) - O(1)$ 算法，以及最终的 $O(n) - O(1)$ 算法。

倍增

倍增法预处理 $f[i][u]$ 表示结点 $u$ 向上 $2^i$ 个祖先结点，其中 $f[0][u]$ 正是父亲，其余部分遵循递推式

$f[i][u] = f[i-1][f[i-1][u]]$

对于一组询问 $(u, k)$，考察 $k$ 的二进制分解 $2^{a_i}+2^{a_2}+\dots + 2^{a_m}$，我们可以利用不超过 $O(\log n)$ 次跳跃到其第 $k$ 个祖先。

长链剖分

$O(n)-O(\log n)$ 算法

长链剖分是这样一种分解：定义树的高度为最深叶子的深度，我们将每个结点于其最高的儿子之间的边标为重边，将其余边标为轻边，那么重边就构成了对树的一个链划分。这个划分有如下的性质：

轻儿子的深度之和 $\le n$。将轻儿子的深度附着在这个轻儿子的重链上，显而易见每一条重链只会提供 $1$ 的贡献，因此轻儿子深度之和 $\le n$。
结点 $u$ 的 $k$ 祖先 $g$ 所在的重链长度至少是 $k$。若不然，$g\to u$ 构成了一条更高的链。

我们将每条长度为 $L$ 的重链预处理出其上方 $L$ 个结点，称为这个重链的上部，这样预处理复杂度仍是 $O(n)$ 的。考虑下面的算法：

对于询问 $(u, k)$，若 $k$ 祖先仍在重链和其上部之内，查表得到 $k$ 祖先
否则，跳到重链上部的顶端，并更新 $u$ 和 $k$

由于每次跳到重链上部的顶端后，所在重链的长度至少 $\times 2$，因此这样的算法时间复杂度是 $O(\log n)$ 的。

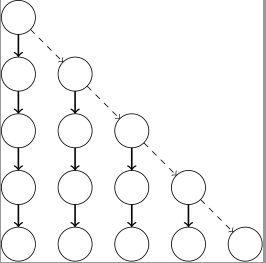
如果不预处理上部，仅仅每次跳到重链顶端的话，算法的时间复杂度将是 $O(\sqrt n)$ 的。一方面，由于每次跳跃后重链长度必然增加，当重链长度小于 $\sqrt n$ 时仅会跳跃 $O(\sqrt n)$ 次，当重链长度大于 $\sqrt n$ 时仅存在不超过 $O(\sqrt n)$ 条不同的重链；另一方面，我们可以构造如下的树将算法的时间复杂度卡到 $\Omega(\sqrt n)$：

$O(n\log n)-O(1)$ 算法

要获得更好的询问时间复杂度可以结合以上两个算法：

用 $O(n\log n)$ 的时间复杂度预处理倍增表 $f[i][u]$
预处理长链剖分，并计算每条长链的上端
对于询问 $(u, k)$，设 $k$ 二进制下的最高位是 $d$，跳到 $f[d][u]$。根据上面的性质 $2$，一定可以通过在长链及其上端查表得到 $k$ 祖先。

这样时间复杂度就被降低到了 $O(n\log n) - O(1)$。

线性时间优化

使用分块技巧可以将预处理的时间复杂度降低到 $O(n)$。设 $b = \lg n / 4$，利用如下算法在树中选出 $O(n/b)$ 个关键点，并使得删去关键点后每一部分大小都不超过 $b$。

在 dfs 处理结点 $nd$ 的过程中，如果子树大小小于 $b$ 则不处理，否则将 $nd$ 选为关键点，并删去整个子树。

一方面利用离线 $O(n+q)$ 算法计算出所有关键点的倍增表，其中 $q = n/b\times \log n = O(n)$；另一方面我们预处理所有节点数小于 $b$ 的树 $T$ 所有可能的询问。由于 $a$ 个节点的树可以对应于 $2a$ 个括号组成的括号序列，因此树的个数不会超过

$2^{2b} = O(\sqrt n)$

表的总大小为

$O(\sqrt n)\times b^2 = O(\sqrt n\log^2 n) = o(n)$

对于一个询问 $(u, k)$，如果答案在块内则查表计算，否则可以转化为关键点上的询问——这可以用倍增表和长链剖分在 $O(1)$ 的时间复杂度内完成。

Note：¹中给出了一种更简单的分块方法。

实现

~~事实上我已经两次尝试写树上四毛子了~~。相比树上并查集实现起来要容易一些，因为并不需要保证联通块个数的界，只需让关键点不太多即可。下载代码

可以使用 CMake 编译运行：

1
2
3

$ cmake .
$ make
$ ./main

其中 src/tree 是树的实现，src/brute 是作为对照的倍增算法，src/std/jump_pointer.h 和 src/std/ladder.h 分别是分块和长链剖分的实现。

由于常数太大，朴素的实现并不会比倍增更好，可能需要精细的卡常。

参考文献

¹. MIT 6.851, Advanced Data Structure, Static tree(1) ↩